INTRO
잘 아려진 BBST(Balanced Binary Search Tree : 균형이진탐색트리)의 종류로는 rb tree, b tree 등이 있습니다.
그러나 위의 rb tree와 같이 대부분의 연산을 \(O(logN)\)에 처리하는 트리는 동작 자체도 복잡하고 구현량이 많기 때문에
직접 구현해가며 PS에 사용하기 어렵습니다. (stl에 있는 것을 가져다 쓰면 좋겠지만 연산을 변형해야하는 경우도 존재하니까요)
그래서 삽입, 삭제 등의 연산에 amortized \(O(logN)\)의 시간복잡도를 가지며 상대적으로 구현량이 적은
Splay Tree를 가장 많이 사용합니다.
하지만 Splay Tree도 zig-zag step 등 헷갈릴만한 요소가 많아서 저는 Treap을 선호합니다.
Treap은 일반적인 \(O(N)\) BST와 구현의 형태가 거의 동일하지만
랜덤을 사용해 \(E(N) = logN\) 시간복잡도를 가지는 자료구조입니다.
이는 랜덤 함수의 특정 시드를 저격하는 것이 아니라면 반례를 만드는 것이 불가능에 가깝기 때문에
\(O(logN)\)이라 생각하고 문제를 풀어도 무방합니다.
이렇게 Treap은 Splay Tree의 연산 대부분을 비슷한 시간복잡도로 지원하며
또 구현이 굉장히 직관적이기에 Splay Tree의 대체제로 훌륭하다 생각합니다.
참고
Randomize Search Trees (Raimund Seidel)
https://infossm.github.io/blog/2019/07/22/Treap/
Concept
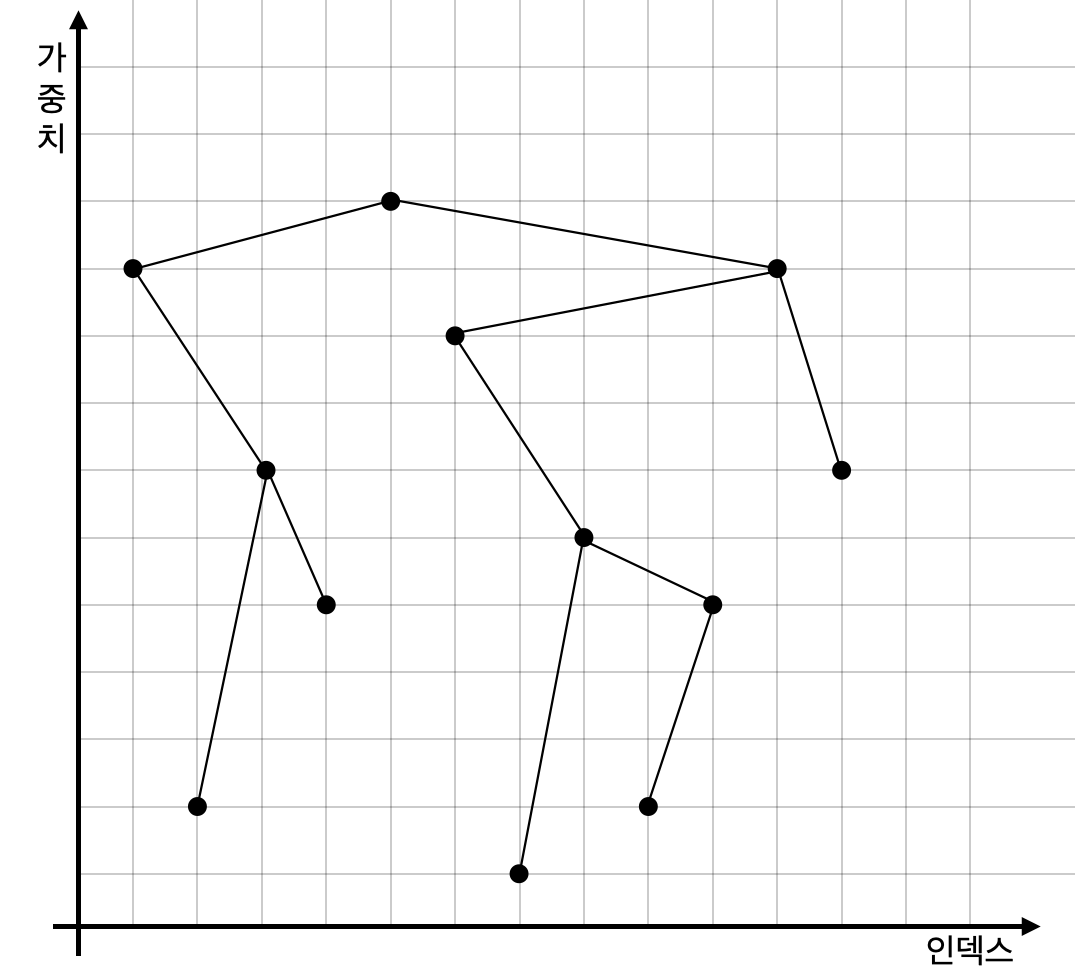
Treap은 Cartesian Tree입니다. 여기서 Cartesian Tree는 중위순회했을 때 원분 수열을 얻을 수 있으며
항상 부모가 자식보다 작거나 그 반대인 Heap의 성질을 만족하는 트리를 의미합니다.
여기서 어떤 것을 기준으로 Cartesian Tree인지가 특이한데, 정점마다의 고유한 가중치를 아무렇게나 만들어줍니다.
아래의 코드의 NODE의 정의에는 val, priority라는 변수가 존재합니다.
여기서 트리에 삽입하고자 하는 원소가 val이며 위 설명의 가중치가 priority입니다.
struct NODE {
int val, priority;
NODE *l, *r;
NODE() {}
NODE(int _val) : val(_val), priority(rand()) {}
};
이렇게 랜덤한 가중치를 부여하여 Cartesian Tree를 만들면 그 높이가 평균 \(logN\)이며
이 때문에 평범한 \(O(N)\) 구현 BST로 보이는 트리에서 다양한 연산들을 평균 \(logN\)에 수행할 수 있습니다.
Time Complexity
시간복잡도가 평균 \(logN\)인 이유를 알아보겠습니다.
Treap의 아무 원소나 골라 root라 잡고 N은 root 서브트리의 크기 + 1이라 정의합니다.
Treap은 Cartesian Tree이기 때문에 원본수열에서 root의 인덱스는 왼쪽 서브트리의 크기 + 1일 것이고 이를 r이라 하겠습니다.
찾고싶은 원소가 왼쪽 서브트리에 있을 확률은 \( \frac{r - 1}{N} \), 루트에 있을 확률은 \(\frac{1}{N}\),
오른쪽 서브트리에 있을 확률은 \( \frac{N - r}{N} \)입니다.
그러면 한단계 내려갔을 때 찾고자하는 원소가 될 수 있는 후보의 개수의 기댓값을 구하면 아래와 같습니다.
("한단계 내려갔을 때"이기 때문에 루트일 경우는 고려하지 않습니다)
\( E(N, r) = (r - 1) \times \frac{r-1}{N} + (N - R) \times \frac{N-R}{N} = \frac{(r - 1)^2 + (N - r)^2}{N} \)
랜덤 함수의 분포가 균일하다면 r이 될 수 있는 값의 확률은 1부터 N 모두 \(\frac{1}{N}\)입니다.
따라서 모든 r에 대해 평균을 구하면 모든 경우를 고려한 기댓값을 구할 수 있습니다.
\( E(N) = \frac{1}{N} \sum_{r=1}^{N}{ \frac{ (r-1)^2 + (N-r)^2 }{N}} \)
\(E(N) = \frac{2N^2 - 3N + 1}{3N} \)
\( \lim_{N \to \infty}{ E(N) } = \lim_{N \to \infty}{ \frac{2N^2 - 3N + 1}{3N} } = \lim_{N \to \infty}{ \frac{2}{3}N } \)
따라서 Treap의 깊이는 평균 \(log_{3/2}N\)이고 이 때문에 삽입, 삭제, 구간 쿼리 등의 연산을 평균 \(logN\)에 해결할 수 있습니다.
* 퀵소트의 평균시간복잡도가 \(NlogN\)인 것도 비슷하게 보일 수 있습니다.
Merge
Merge는 Treap 두개를 하나로 합치는 연산입니다.
Merge(left, right)는 left와 right중 가중치가 큰 정점을 루트로 만들고 나머지 하나를 그 아래에 붙입니다.
이 때 합쳐진 Treap에서는 모든 left의 원소가 right보다 왼쪽에 위치해야합니다.
아래 구현의 upd 함수는 왼쪽 자식과 오른쪽 자식의 사이즈 합 + 1을 자신의 사이즈값으로 갱신합니다.
자식들에 변화가 있을 때마다 upd를 호출해야합니다.
시간복잡도 : \(O(logN)\)
NODE *Merge(NODE *x, NODE *y) {
if(x == 0) return y;
if(y == 0) return x;
if(x->pr < y->pr) {
x->r = Merge(x->r, y);
return x->upd();
} else {
y->l = Merge(x, y->l);
return y->upd();
}
}
Split
하나의 Treap을 왼쪽 k개와 오른쪽의 나머지로 분리하는 함수입니다.
1. 현재 정점이 k번째라면 {왼쪽 서브트리 + 자신, 오른쪽 서브트리}로 분할합니다.
2. 왼쪽 서브트리의 크기가 k이상이라면 {왼쪽 서브트리에서 왼쪽 k개, 남은 것 + 자신 + 오른쪽 서브트리}로 분할합니다.
3. 오른쪽 서브트리에 k번째 정점이 존재한다면
{왼쪽 서브트리 + 자신 + 오른쪽에서 k-(왼쪽 서브트리 크기 + 1)개, 나머지}로 분할합니다.
세그먼트 트리에서 k번째 수를 구하는 연산과 형태가 비슷합니다.
만약 문제의 조건에 의해 부모 노드의 주소를 저장한다면 Split에서 이를 끊어주는 것도 중요합니다.
시간복잡도 : \(O(logN)\)
pair<NODE*, NODE*> Split(NODE *x, int k) {
if(x == 0) return {0, 0};
if(getsize(x->l) + 1 == k) {
auto r = x->r;
x->r = 0;
return {x->upd(), r};
} else if(getsize(x->l) >= k) {
auto [l, r] = Split(x->l, k);
x->l = r;
return {l, x->upd()};
} else {
auto [l, r] = Split(x->r, k - getsize(x->l) - 1);
x->r = l;
return {x->upd(), r};
}
}
Flip
구간 [l, r]을 뒤집는 방법은 간단합니다.
Treap을 [1, l), [l, r], (r, N] 3개로 분리한 후 [l, r]의 flip값을 반전시켜줍니다.
flip 값은 lazy propagation으로 관리하며 해당 노드에 접근할 때마다 전파해야합니다.
전파는 다음과 같이 구현할 수 있습니다.
시간복잡도 : \(O(logN)\)
struct NODE {
~~~~~~~~~~ 생략
void push() {
if(flip) {
swap(l, r);
if(l) l->flip ^= 1;
if(r) r->flip ^= 1;
flip = 0;
}
}
};
Shift
[l, r]을 오른쪽으로 x만큼 shift하는 방법은 다음과 같습니다.
1. Treap을 [1, l), [l, r-x+1], (r-x+1, r], (r, N]으로 분리합니다.
2. Treap을 [1, l), (r-x+1, r], [l, r-x+1], (r, N]순으로 합칩니다.
Flip 3번을 통해서도 구간 shift가 가능하지만 Split 6번, Merge 6번이 필요하기 때문에 위 방법보다 느립니다.
시간복잡도 : \(O(logN)\)
auto [p, l] = Split(root, s - 1);
auto [r, q] = Split(l, e - s + 1);
x %= e - s + 1;
if(x) {
auto [a1, a2] = Split(r, (e - s + 1) - x);
r = Merge(a2, a1);
}
root = Merge(p, r);
root = Merge(root, q);
Test
Splay Tree 기초 문제로 잘 알려져있는 [BOJ 13159] 배열에 테스트해봤습니다.
이 문제는 임의의 구간 [l, r]에 대해 최소, 최대, 합을 구하는 연산과, 임의의 원소 하나를 수정하는 연산을
모두 대략 \(logN\)시간 이하에 처리해야 시간제한에 통과할 수 있습니다.
Treap으로 풀기위해선 a[i] = x인 i를 찾는 것에서 부모를 저장할 필요가 있는데
이 부모-자식 관계를 Split, Merge에서 잘 처리하는 것이 중요합니다.
#include "bits/stdc++.h"
#define endl '\n'
using namespace std;
using ll = long long;
struct RAND {
random_device rg;
mt19937 rd;
RAND() { rd.seed(rg()); }
int nxt(int l=0, int r=1000000000) { return uniform_int_distribution<int>(l, r)(rd); }
} rnd;
struct NODE {
NODE *l, *r, *par;
int pr, sz, val, flip;
int mx, mn; ll sum;
NODE(int _val=0) {
l = r = par = 0;
pr = rnd.nxt();
sz = 1; flip = 0;
val = sum = mn = mx = _val;
}
void push() {
if(flip) {
swap(l, r);
if(l) l->flip ^= 1;
if(r) r->flip ^= 1;
flip = 0;
}
}
NODE *upd() {
push();
sum = mx = mn = val; sz = 1;
if(l) {
l->par = this;
sz += l->sz;
sum += l->sum;
mn = min(mn, l->mn);
mx = max(mx, l->mx);
}
if(r) {
r->par = this;
sz += r->sz;
sum += r->sum;
mn = min(mn, r->mn);
mx = max(mx, r->mx);
}
return this;
}
};
int getsize(NODE *x) {
if(x == 0) return 0;
else return x->sz;
}
NODE *Merge(NODE *x, NODE *y) {
if(x == 0) return y;
if(y == 0) return x;
x->push(); y->push();
if(x->pr < y->pr) {
x->r = Merge(x->r, y);
return x->upd();
} else {
y->l = Merge(x, y->l);
return y->upd();
}
}
pair<NODE*, NODE*> Split(NODE *x, int k) {
if(x == 0) return {0, 0};
x->push();
if(getsize(x->l) + 1 == k) {
auto r = x->r;
x->r = 0;
if(r) r->par = 0;
return {x->upd(), r};
} else if(getsize(x->l) >= k) {
auto [l, r] = Split(x->l, k);
x->l = r;
if(l) l->par = 0;
return {l, x->upd()};
} else {
auto [l, r] = Split(x->r, k - getsize(x->l) - 1);
x->r = l;
if(r) r->par = 0;
return {x->upd(), r};
}
}
int getval(NODE *x, int k) {
x->push();
if(getsize(x->l) + 1 == k) return x->val;
else if(getsize(x->l) >= k) return getval(x->l, k);
else return getval(x->r, k - getsize(x->l) - 1);
}
int getidx(NODE *x, NODE *cmp, int f) {
if(x == 0) return 0;
int ret = getidx(x->par, x, 0);
x->push();
ret += x->r == cmp or f ? getsize(x->l) + 1 : 0;
return ret;
}
int n, q;
NODE *root;
NODE *ptr[303030];
void dfs(NODE *x) {
if(x == 0) return;
x->upd();
dfs(x->l);
cout << x->val << ' ';
dfs(x->r);
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
// freopen("input.txt", "r", stdin);
cin >> n >> q;
for(int i=1; i<=n; i++) {
ptr[i] = new NODE(i);
root = Merge(root, ptr[i]);
}
root->par = 0;
while(q--) {
int op; cin >> op;
if(op == 1) {
int s, e; cin >> s >> e;
auto [p, l] = Split(root, s - 1);
auto [r, q] = Split(l, e - s + 1);
cout << r->mn << ' ' << r->mx << ' ' << r->sum << endl;
r->flip ^= 1; r->push();
root = Merge(p, r);
root = Merge(root, q);
}
if(op == 2) {
int s, e, x; cin >> s >> e >> x;
auto [p, l] = Split(root, s - 1);
auto [r, q] = Split(l, e - s + 1);
cout << r->mn << ' ' << r->mx << ' ' << r->sum << endl;
if(x >= 0) {
x %= e - s + 1;
if(x) {
auto [a1, a2] = Split(r, (e - s + 1) - x);
r = Merge(a2, a1);
}
} else {
if(x) {
x = -x;
x %= e - s + 1;
auto [a1, a2] = Split(r, x);
r = Merge(a2, a1);
}
}
root = Merge(p, r);
root = Merge(root, q);
}
if(op == 3) {
int idx; cin >> idx;
cout << getval(root, idx) << endl;
}
if(op == 4) {
int x; cin >> x;
cout << getidx(ptr[x], 0, 1) << endl;
}
root->par = 0;
}
dfs(root);
}'알고리즘, 자료구조' 카테고리의 다른 글
| Path Comprssion DSU의 amortized O(logN) 증명 (2) | 2023.04.19 |
|---|---|
| Simulated Annealing (1) | 2022.02.01 |
| Efficient Range Minimum Queries using Binary Indexed Trees (0) | 2022.01.21 |


