주제 : 역원이 존재하지 않는 연산에 대한 구간 쿼리 (펜윅 트리)
펜윅트리에서 요구하는 연산을 $, 이 연산의 역원을 #라고 정의하겠습니다.
흔히 펜윅트리에서 구간 [L, R]에 대한 쿼리를 처리할 때는 ([1, R] 쿼리의 답) # ([1, L) 쿼리의 답)과 같은 형태로 답을 구합니다.
$이 +라고 한다면 #은 -로 ([1, R] 쿼리의 답) - ([1, L) 쿼리의 답)을 의미합니다.
역원이 존재하지 않는 연산은 어떻게 처리해야할까요?
그 예로 \( min(a, ?) = \infty \)를 만족하는 ?는 존재하지 않기 때문에
min에는 역원이 존재하지 않습니다.
그래서 일반적인 형태의 펜윅 트리로는 구간 [L, R]의 min값을 구할 수 없습니다.
이제 펜윅트리로 range rmq 문제를 해결하는 방법을 알아보겠습니다.
출처는 아래의 Efficient Range Minimum Queries using Binary Indexed Trees입니다.
https://ioinformatics.org/journal/v9_2015_39_44.pdf
1. Binary Indexed Tree의 이해
* LSB(i) = i의 켜진 비트 중 가장 작은 것의 위치
* x & -x는 \(2^{LSB(x)}\)와 같습니다.
1. 펜윅트리의 i번 정점은 구간 (i - (i & -i), i]를 관리합니다.
따라서 펜윅트리의 쿼리 형태가 아래와 같습니다.
while(i > 0) {
ret += tree[i];
i -= i & -i;
}
현재 구간 (i - (i & -i), i]를 처리하고 i - (i & -i)를 오른쪽 끝으로 하는 다음 구간들을 계속 처리해나가는 것입니다.
켜진 비트를 하나씩 꺼나가기 때문에 시간복잡도는 \(O(logN)\)입니다.
펜윅트리의 i번 정점이 구간 [i, i + (i & -i))를 관리하도록 할 수는 없을까? 가능합니다.
이것이 펜윅트리로 구간쿼리를 처리하기 위해 필요한 핵심 아이디어입니다.
2. 펜윅트리는 binomial tree입니다.
binomial tree는 아래와 같이 자기 자신과 똑같은 형태의 트리를 자식으로 이어붙임으로서 귀납적으로 정의되는 트리입니다.
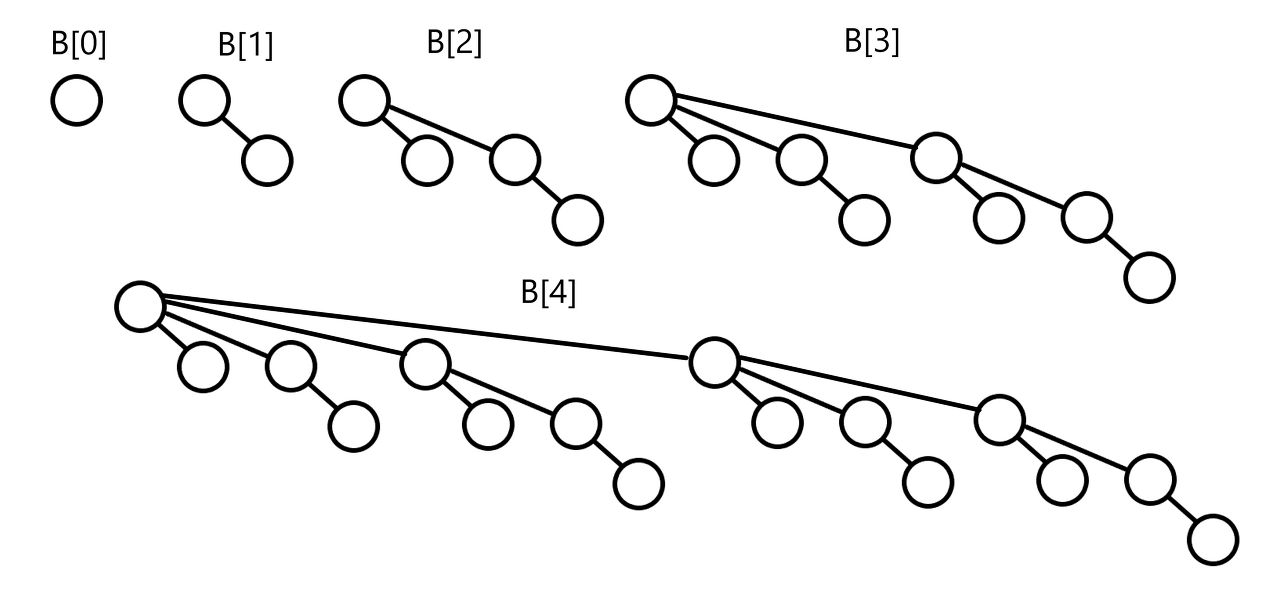
3. 펜윅트리의 정점에서 자식 정점과 부모 정점은 어떻게 구할까?
정점마다 (i - (i & -i), i]를 관리하는 펜윅트리에서는 i + (i & -i)를 통해 부모 정점을 구할 수 있으며
자식들은 \( 1 \leq 2 ^ j < i \)& \(-i\)인 j들에 대해 \( i - 2^j \)입니다.
정점마다 [i, i + (i & -i))를 관리하는 펜윅트리에서는 i - (i & -i)를 통해 부모 정점을 구할 수 있으며
자식들은 \( 1 \leq 2 ^ j < i \)& \(-i\)인 j들에 대해 \(i + 2 ^ j\)입니다.
부모 정점이 관리하는 구간은 자식 정점들이 관리하는 구간들의 합이기 때문에 자식 정점들의 값을 통해
부모 정점의 값을 결정할 수 있습니다.
쿼리
구간 [L, R]에 대한 쿼리에 대해 실제 [L, R]을 관리하는 정점들을 통해서만 답을 구해내야합니다.
(i - (i & -i), i]를 관리하는 펜윅트리를 A, [i, i + (i & -i))를 관리하는 펜윅트리를 B라고 하겠습니다.
이 때 쿼리를 해결하는 방법은 다음과 같습니다.
1. L부터 L += L & -L을 하면서 L + (L & -L) <= R을 만족하는 동안 B[L]을 답에 갱신해줍니다.
2. R부터 R -= R & -R을 하면서 R - (R & -R) >= l을 만족하는 동안 A[R]을 답에 갱신해줍니다.
3. 답에 v[R]을 갱신합니다.
이것이 비는 구간없이 모든 구간의 값을 체크할 수 있고 중복되는 점을 갱신하지 않는 것이 보장된다면
이는 rmq뿐만 아니라 모든 연산에 대해 정상적으로 작동할 것입니다.
그렇다면 조건을 만족하는 마지막 L + (L & -L) + 1이 조건을 만족하지 않는 첫 R과 같으면 됩니다.
이 첫 R을 p라고 하겠습니다. 과정 1은 구간 [L, p)를 처리할 것이며 과정 2는 구간 (p, R]을 처리해야합니다.
위의 논문을 통해 이 p가 항상 존재, 유일하며 그 위치가 L ^ R의 MSB임을 알 수 있습니다.
* MSB = 켜져있는 최상단 비트
T qry(int l, int r) {
T ret1 = ID, ret2 = ID; int i;
for(i=l; i+(i&-i)<=r; i+=i&-i) ret2 = f(ret2, FT2[i]);
for(i=r; i-(i&-i)>=l; i-=i&-i) ret1 = f(FT1[i], ret1);
return f(f(ret1, v[i]), ret2);
}업데이트
업데이트가 조금 어렵습니다.
A에서 부모가 있는 정점 i를 보겠습니다. 이 i에서 관리하는 구간은 (i - (i & -i), i]이며
부모인 i + (i & -i)가 관리하는 구간은 항상 i의 구간을 포함합니다. 따라서 부모로 이동할수록
구간의 L은 단조감소하며 R은 단조증가합니다.
이 아이디어로 갱신할 부모마다 자식의 구간을 투포인터처럼 관리하면 업데이트를 \(O(logN)\)에 구현할 수 있습니다.
void upd(int i, T x) {
T t = v[i] = x;
for(int j=i,l=i-1,r=i+1; j<=n; j+=j&-j) {
while(l > 0 and l - (l & -l) >= j - (j & -j)) t = f(FT1[l], t), l -= l & -l;
while(r + (r & -r) <= j) t = f(t, FT2[r]), r += r & -r;
FT1[j] = i ^ j ? f(t, v[j]) : t;
}
t = x;
for(int j=i,l=i-1,r=i+1; j>0; j-=j&-j) {
while(l - (l & -l) >= j) t = f(FT1[l], t), l -= l & -l;
while(r + (r & -r) <= j + (j & -j)) t = f(t, FT2[r]), r += r & -r;
FT2[j] = i ^ j ? f(v[j], t) : t;
}
}정리
펜윅 트리의 장점은 메모리를 덜 사용한다는 점과 시간복잡도의 상수가 매우 작다는 점에 있습니다.
하지만 위 펜윅 rmq는 잘 구현된 비재귀 세그먼트 트리와 비교했을 때 쿼리에서는 빠르나 업데이트에서 조금 느립니다.
그래서 쿼리가 압도적으로 많은 경우에만 이득을 볼 수 있을 듯합니다.
그리고 금광 세그와 같이 결합법칙은 성립하지만 교환법칙이 성립하지 않는 경우가 있으니 조심해야합니다.
PS. 도와주신 jinhan814님 감사합니다!
http://boj.kr/02d6726e158044b29ed0b17507e42ccd : 연속합과 쿼리
전체코드
template<typename T>
struct fenwick {
int n; T ID; vector<T> v, FT1, FT2;
function<T(const T&, const T&)> f;
fenwick() {}
fenwick(int _n, T _ID, function<T(const T&, const T&)> _f) : n(_n), ID(_ID), f(_f) {
// FT1[j] = (j - (j & -j), j]
// FT2[j] = [j, j + (j & -j))
FT1 = vector<T>(n + 1, ID);
FT2 = vector<T>(n + 1, ID);
v = vector<T>(n + 1, ID);
}
void init() {
for(int i=1; i<=n; i++) if(i + (i & -i) <= n)
FT1[i + (i & -i)] = f(FT1[i], FT1[i + (i & -i)]);
for(int i=n; i>0; i--)
FT2[i - (i & -i)] = f(FT2[i], FT2[i - (i & -i)]);
}
void upd(int i, T x) {
T t = v[i] = x;
for(int j=i,l=i-1,r=i+1; j<=n; j+=j&-j) {
while(l > 0 and l - (l & -l) >= j - (j & -j)) t = f(FT1[l], t), l -= l & -l;
while(r + (r & -r) <= j) t = f(t, FT2[r]), r += r & -r;
FT1[j] = i ^ j ? f(t, v[j]) : t;
}
t = x;
for(int j=i,l=i-1,r=i+1; j>0; j-=j&-j) {
while(l - (l & -l) >= j) t = f(FT1[l], t), l -= l & -l;
while(r + (r & -r) <= j + (j & -j)) t = f(t, FT2[r]), r += r & -r;
FT2[j] = i ^ j ? f(v[j], t) : t;
}
}
T qry(int l, int r) {
T ret1 = ID, ret2 = ID; int i;
for(i=l; i+(i&-i)<=r; i+=i&-i) ret2 = f(ret2, FT2[i]);
for(i=r; i-(i&-i)>=l; i-=i&-i) ret1 = f(FT1[i], ret1);
return f(f(ret1, v[i]), ret2);
}
};'알고리즘, 자료구조' 카테고리의 다른 글
| Path Comprssion DSU의 amortized O(logN) 증명 (2) | 2023.04.19 |
|---|---|
| Simulated Annealing (1) | 2022.02.01 |
| Randomize Binary Search Trees, Treap (3) | 2022.01.25 |


